MoneroのRingCTに使われる署名の基本となるLWWのLSAGについて - SaaSベンチャーで働くエンタープライズ部長のブログ

f:id:naomasabit:20201223003118p:plain

MoneroのRing Confidential Transactionによって利用された技術にMLSAGがありますが、元となった技術としてLWWのLSAG(Linkable Spontaneous Anonymous Group)があります。これはAdam Backが修正を加えることでRingCT利用可能だと伝えたものです。

MLSAGについてもまとめますが、まず基礎知識としてLWWのLSAGについてまとめます。元論文はMonero Research Labが出しているRing Confidential Transactionのペーパーです。

リング署名について
LWW のLSAGの署名
LWW のLSAGの署名検証
キーイメージの利用方法
参考

リング署名について

事前知識としてまずリング署名の基礎について触れます。リング署名をとても雑に表現すると、Ｎ人のメンバーがいる時、ランダムな値とダミーの公開鍵を用いて順番に署名していきます。

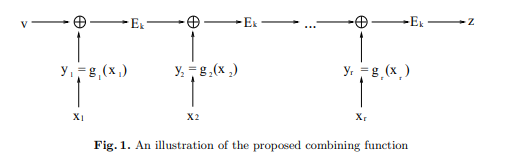
f:id:naomasabit:20201220224224p:plain — リング署名 - 順番に署名していく図

得られた最後の一人の署名を用い、自身の秘密鍵を用いて署名を行うと最初の値になるように値を調整することで循環するリングを作成します。この形を作成することで、第3者からはリング参加者の誰かが秘密鍵署名者であることはわかりつますが、誰かは特定することはできません。

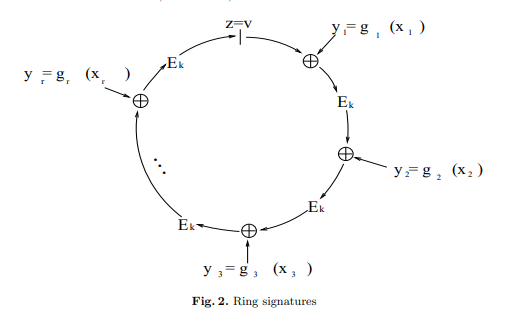
f:id:naomasabit:20201220224058p:plain — リング署名図

これらの図は「How To Leak a Secret」というリング署名の提案がされた古典論文より引用しています。

LWW のLSAGの署名

LWWのLSAGはリング署名を基にした形です。利用される用語を以下にまとめています。

f:id:naomasabit:20201220230009p:plain — 用語集

まず、最初にα、参加者n人全員のダミー公開鍵 $P _ 1, ..., P _ n$ ,ランダムな数値 $s _ i$ , $i \in \{1,....,n \} , i \neq n$ を用意します。

jからスタートし、

$L_j = αG$ , $R_j = αH_p(P_j)$ を計算します。
次に $L_j, R_j$ から $c_{j+1} = h(m,L_j,R_j)$ を計算します
$c _ {j+1}$ をもちいて $L _ {j+1} = s _ {j+1}G+c _ {j+1}P _ {j+1}$ , $R _ {j+1}=s _ {j+1}{H _ p}P _ {j+1} + c _ {j+1}I$ を計算します
2同様に $c _ {j+2}$ を計算します。
3同様に $L _ {j+2}, R _ {j+2}$ を計算します。

4,5を繰り返して $j-1$ まで計算したら、 $s _ j$ を $s _ j = α - c _ i x _ i modl$ となるように調整します。 $l$ はed25519の定数である素数。 $l=2^ {252}+27742317777372353535851937790883648493$

そのように計算した結果が下図で $L _ j = αG$ , $R _ j = α H _ p(P _ j)$ となり、 $L _ j, R _ j$ がリング状になります。

$L_j, R_j$ の等式変換は図参照。

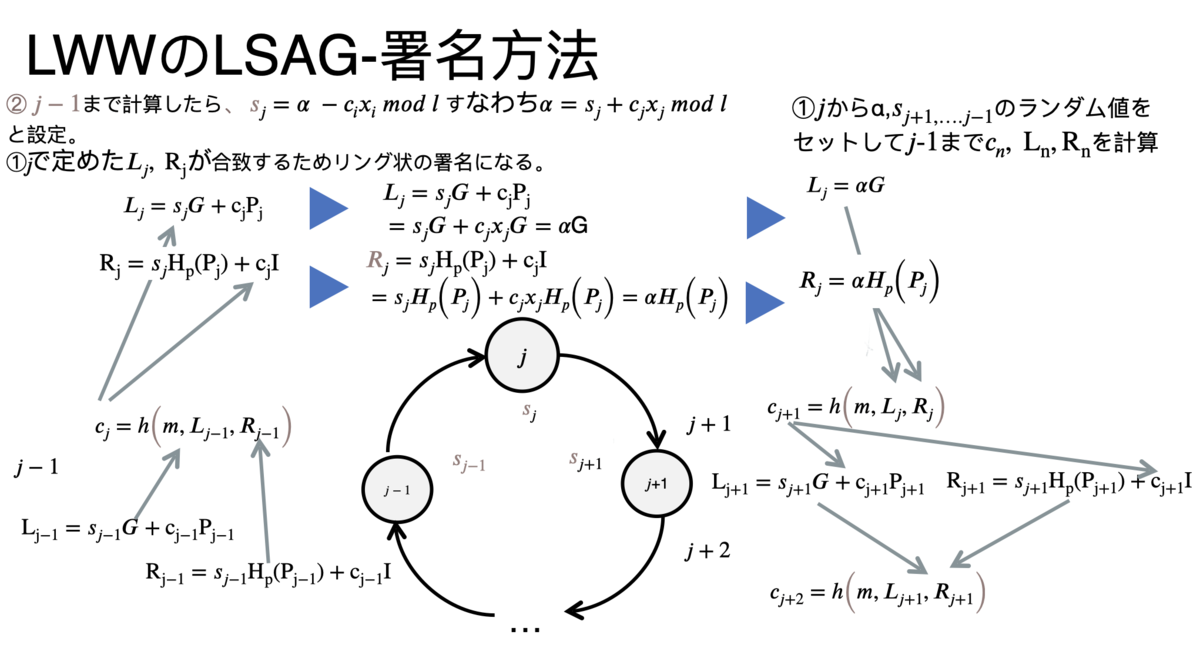
f:id:naomasabit:20210101182934p:plain — LWWのLSAG署名方法

最終的な署名セットは $σ = (I, c _ 1, s _ 1, ... , s _ n)$ となる。

LWW のLSAGの署名検証

検証者は、 $L _ i, R _i, c _ i$ を用いて、 $c _ (i+1) = h(m, L _ i, R _ i)$ を計算し、 $c _ (n+1) = c _ 1$ でリングになっていることを検証する。

キーイメージの利用方法

署名 $σ = (I, c _ 1, s _ 1, ... , s _ n)$ のうち、 $I$ はコインの二重使用を防ぐために利用します。署名者の鍵からキーイメージを計算することで、同一のキーイメージが利用されたらそれは秘密鍵の二重使用とみなす。Moneroはアドレスは使い捨てのため、秘密鍵を二回利用するすなわちコインの二重使用とみなし、不正送金とする。

これを前提にしてMLSAGを次の記事は解説していきます。

参考

techmedia-think.hatenablog.com